The construction of a typical horizontal sundial
A typical horizontal sundial consists of three parts: the gnomon casting shadow on a dial, a dial on which the shadow falls and the sun itself. The lines on a dial, the shape and size of the gnomon depend on the geographical coordinates of the place where the sundial is installed. The sundial is an astronomical instrument designed to measure the altitude, azimuth and declination of the sun. The dimension of these variables are degrees of arc. At its discretion, we can give them a different physical meaning. Thus, according to the value of the azimuth we can measure the time. Using the value of the sun declination, we can learn the date of the sun transition from one zodiac constellation to another, to determine the day of the equinox, solstice or any other date, such as a birthday.
Location of lines on the face of a sundial depends on the orientation of the dial relative to the pole, the mathematical horizon and the celestial equator. The dial can be drawn anywhere, for example on the spherical surface. Despite the fact that the constructions of sundials are extremely diverse, most people believe that the sundial is a disk, to which a triangle is attached. This is partly true. That is what a common horizontal sundial looks like.
Let us consider of what parts a typical horizontal sundial consists.
The scales.
The main element of the dial is the scale to measure the time. Accuracy of the scale depends on the accuracy of the sundial assembling and its size. The larger its size is the more precise the scale is. The scale intervals are segments of the hour lines formed by the gnomon shadow on the dial face. In the photograph below the hour lines are highlighted.
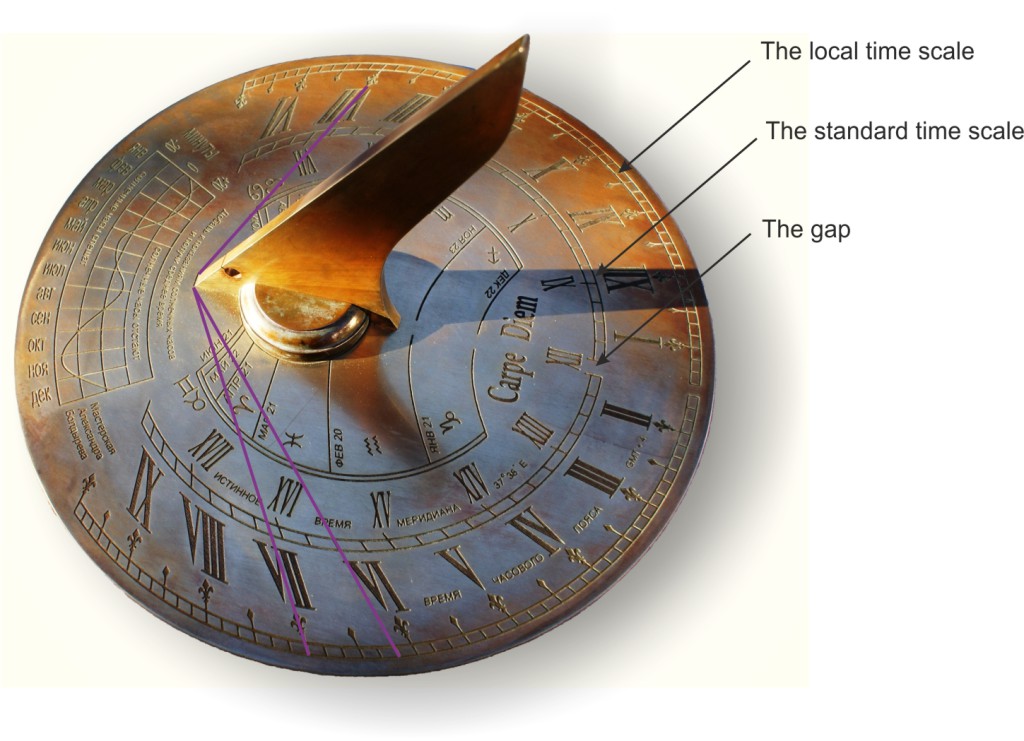
The sundial with two scales for measuring time in terms of the true local time and standard daylight saving time.
Earlier, before the widespread use in everyday life of the world zone standard time, it was enough to design only one scale measuring the true local time — that is, the time at the meridian where the sundial is set. Now you can see on the dials two or even three scales. The first is to measure the local time; the second is to measure the standard time; ant the third is to measure the standard time in terms of daylight saving time. This is done so as not to discomfort the user with computing. Whatever the case it may, I do it just for this purpose. It should be borne in mind that these are not different kinds of time, and they are just the different ways of measuring the same thing.

The sundial for time zones GMT + 3 and GMT + 1
Sometimes it is necessary to add an additional scale on the dial face. The need for this arises when the sundial is intended to measure the time in a time zone, distant from the place of its installation of thousands kilometers. For example, this sundial is set in the city of Umea (Sweden) but measures the time in Moscow.

The scale of azimuths of the sun and the scale of its altitude
Sometimes, besides scales measuring time, a sundial may have the longitude scale and the scales for measuring the solar azimuth and the solar altitude.
Azimuth is an angle between the direction to the Pole and the direction to a remote object. In gnomonica, unlike geodesy, the azimuth is usually measured from the direction to the south geographic pole. This means that at the time of true solar noon the sun azimuth is equal 180º by definition, and in that moment, when the sun is exactly in the west or in the east, its azimuth is equal 90º and -90º respectively. Most people believe that the sun always rises in the east and sets in the west. On a scale of azimuths is easy to see that this is not truth. Only twice a year, at the equinoxes, the sun rises in the east and sets in the west.
The scale measuring the sun altitude is usually placed at the face of a sundial designed to serve as a visual aid. In everyday life, there is no need to know what the sun altitude is. However, on a sundial mounted in the school yard such a scale is appropriate.
Longitude scale allows us to observe the movement of the sun across the planet. When the sun crosses a local meridian a true solar noon is registered. It means that the sun is at the highest point of its daily path and its azimuth is exactly 180º. At this moment, the sun is exactly in the south. If to supplement the scale of longitude with the names of cities so that the name of the city is located next to the corresponding longitude, then the shadow of the gnomon points out in which city the true noon is now.

The scale of longitude supplemented with the names of cities
The equation of time and the analemma.
On a sundial or next to it the table of the equation of time and the analemma are often placed. To understand what they are you need some explaining. The fact is that the readings of a sundial coincide with the readings of a wristwatch only four times a year — April 15, June 12, September 1 and December 24. On other days, a sundial fasts or slows in the range of (+ 14) — (-16) minutes. The reason is that a sundial measure the true objectively existing solar time, while a wristwatch measures the mean time witch people specially invented to simplify the process of its measuring. In everyday life, we use only the mean time. In order to find out the mean time on the reading of a sundial we should add to the reading of a sundial a special correction called the equation of time. Thus, the equation of time is the difference between the readings of a wristwatch and the readings a sundial. In the literature, it is usually denoted as μ or EoT. At different times of the year the value of μ has a different meaning. Expressed graphically, the dependence of μ on the calendar date is called the graph, the nomogram or a table of the equation of time.
The Earth revolves around the sun in the plane called the ecliptic. The axis of rotation of the Earth directed northwards and inclined to this plane at an angle of approximately 23º. This means that in six months we can see that the sun is below the ecliptic. At this period there is the winter in the northern hemisphere. During the other half of the year, we see that the sun is above the ecliptic. At this period there is the summer in the northern hemisphere. Expressed in degrees of arc the height of the sun above or below the ecliptic is called the declination ρ. The graphical dependence of μ from the sun's declination ρ is called the analemma. In the coordinates ρ and μ the analemma is a curve in the shape of the figure eight.

The circular graph of the equation of time and the analemma designed to calculate the mean time on the readings of the sundial.
We can use the analemma in two ways. The first method consist of dividing the analemma into the parts corresponding to calendar dates. Then, if we know what day it is, we can read the coordinate μ and determine how many minutes we are to add to the sundial readings to know what time it is in terms of the conventional mean time. At the same time, by the coordinate ρ, we can learn the value of the sun declination.
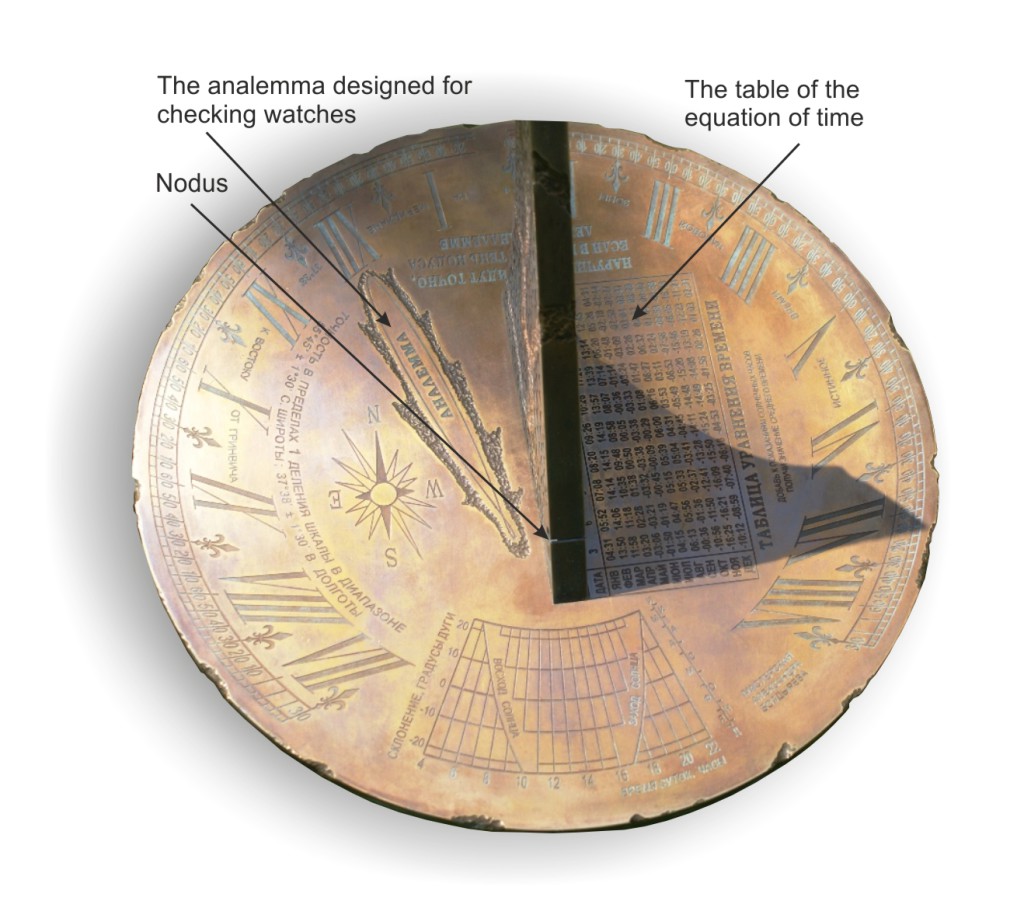
The table of the equation of time and the analemma, located along the hour line. The analemma is used as a tool for verification of mechanical, electronic or any other watches.

The graph of the equation of time can be cut out of stone and placed near the sundial as an art object.
The second method does not require knowledge of the calendar date. In this case, a specifically designed analemma, divided into sections that correspond to calendar dates, is arranged along an hour line. At the time when the shadow of nodus (described below) crosses the analemma (not hour a line!) the reading of the sundial coincide with the mean time, and the point of the analemma crossed by the shadow of nodus corresponds to the calendar date. Located along the hour line, the analemma is very useful tool for checking the mechanical clock, and to determining the calendar date. If the size of a sundial is large enough we can beat the analemma on 365 parts and thus to give to the sundial the function of a perpetual calendar.
The shadow of nodus crosses the «eight» of analemma twice. Therefore, the use the analemma as a tool for verification of watches and to identifying the date assumes that the user knows that the analemma has two parts — winter and summer, and that they are not symmetrical to each other. Graphically, they look like the mirrored to each other S-shaped curves. The winter part of analemma is used in the period between the fall and the spring equinox, the summer one is used in the period between the spring and the fall equinoxes.
There are dozens of ways to graphic the images of EoT and analemma and a great variety of art techniques of doing it. Here are some of them.

A graph and a table of the equation of time can be made of stone and gilded or patinated non-ferrous metal.
The gnomon.
Gnomon is an object that casts shadow on the dial and works like an hour hand in a clock. In the horizontal sundial, it usually has the shape of a triangle, the angle of inclination corresponding to the latitude. Plane of the triangle is parallel to the local meridian; its upper edge is parallel to the Earth's axis and in the northern hemisphere and is always directed toward the North Celestial pole.

The gnomon made of bronze.

The gnomon with textured surface. Brass.
Gnomon is a material object. It has a thickness that should be taken into account when delineating a dial. The break is to be made in scales the width of which is equal to the thickness of the gnomon. Strictly speaking, an accurate sundial has two gnomons – the east one and the west one. The west one is an edge formed by the western and upper faces. It works as a time pointer from 6:00 a.m. to the true noon and after 6:00 p.m. to sunset. The east one is an edge formed by the east and upper faces. It works as a time pointer from sunrise to 6:00 a.m. and from the true noon to 6:00 p.m.

The gnomon with the nodus. On the eastern face of the gnomon the quotation from the novel by Harry Harrison «Steel Rat gets drafted» is etched. Brass, gold 24K.

The gnomon with the nodus. On the west face of the gnomon the quotation from the article by Michael Lomonosov «On the improvement of telescopes», 1762, is etched.
One of the faces of the gnomon is curvilinear. This is done not only for aesthetic reasons but also in order to avoid confusion on which edge to use for registration of time. The gnomon body does not have to be solid. It can be made by means molding, waterjet cutting, or in any other methid depending on preference. It is only important that the face designed to measure time is strictly straight and is placed in reference points of the dial.

Horizontal sundial with two gnomon. On the birthday of the owner the shadow of the cone top goes along the specially calculated anniversary line.
Usually, only one gnomon is set on the sundial. The exception is the Ottoman sundial. It has two gnomons. One of them is for measuring time, the other is to determine the time of Islamic prayers. Sometimes, I install two gnomons on a sundial for special purpose. For example, in this sundial the large gnomon is designed for recording time, while a small cone-shaped one is designed to ensure that once a year, on the birthday of the owner, the shadow of the tip of the cone goes along a special anniversary line.

The sundial with three gnomons.
In very rare cases, more than two gnomons are set on the sundial. For example, this sundial has three circular scales, each of them having its own gnomon. One of them is designed to measure the true local time at the meridian of the place of installation, the other one is designed to measure the true standard time of the time zone, and the third one is to measure the azimuth of the sun.
Nodus. Declination lines. Anniversary line.
Nodus (in Greek — node) is a point on the gnomon, the shadow of which corresponds to the declination of the sun. Declination is the altitude of the sun above the ecliptic. Ecliptic is a plane in which the Earth revolves around the sun.
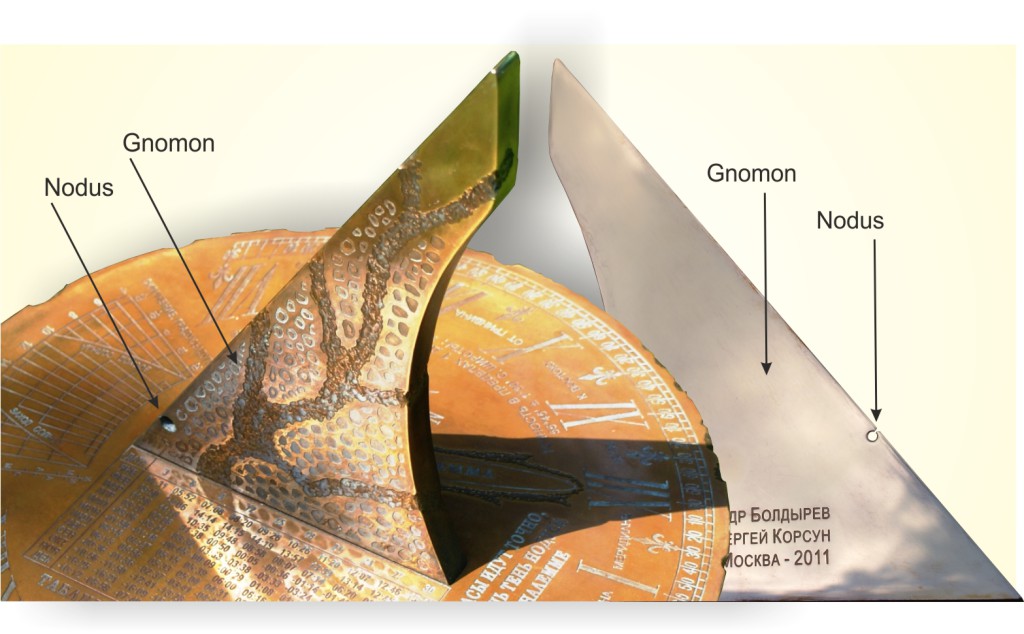
Nodus is usually done in the form of a mark on the polar face of the gnomon.
Every day of the year corresponds to a certain value of the sun declination. As soon as the sun, carrying their day's path, moves from east to west, the shadow of the nodus moves across the dial from west to east. The trajectory of the nodus shadow is unique for each day of the year and does not change significantly over the centuries. This trajectory is called the declination line.
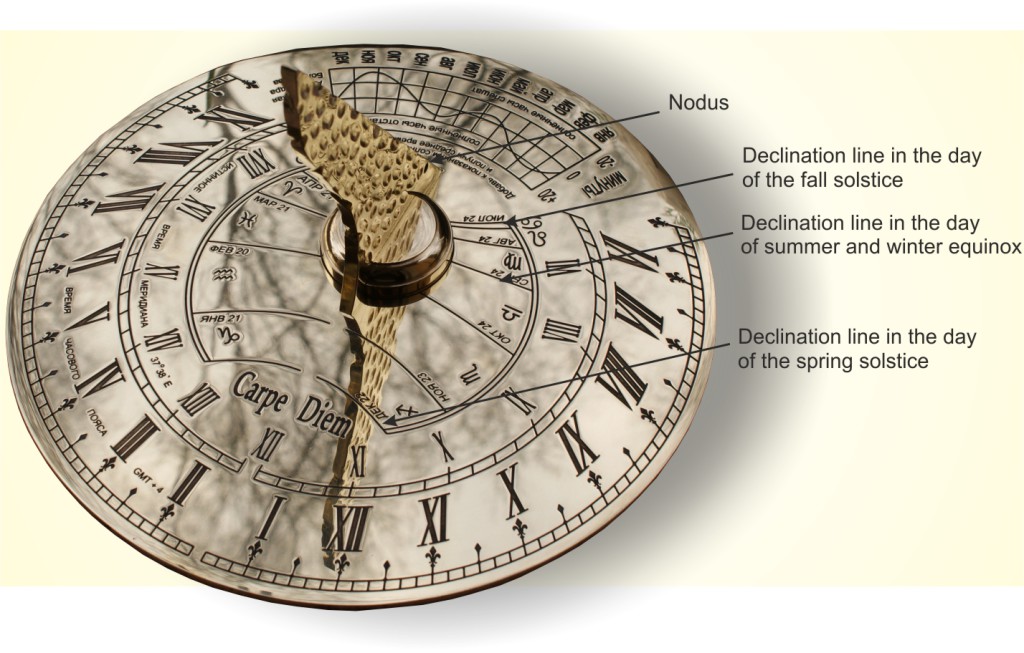
The lines of declination correspond to the date of transition the sun from one zodiac constellation to another.
Declination lines can be calculated for any date. However, they are usually calculated for the dates having astronomical meaning, for example, for the days of equinoxes and solstices. As soon as the Earth makes its annual revolution around the sun the star background of the sun is changed. Since time immemorial, it is divided into twelve 30° divisions, called the Zodiac constellations. Many people still tend to treat the transition of the sun from one Zodiac constellation to another as a significant astronomical event. If the declination lines are calculated for each of the twelve divisions, then the sundial gets one more feature. It can record the dates of the beginning and the end of the Zodiacal months.
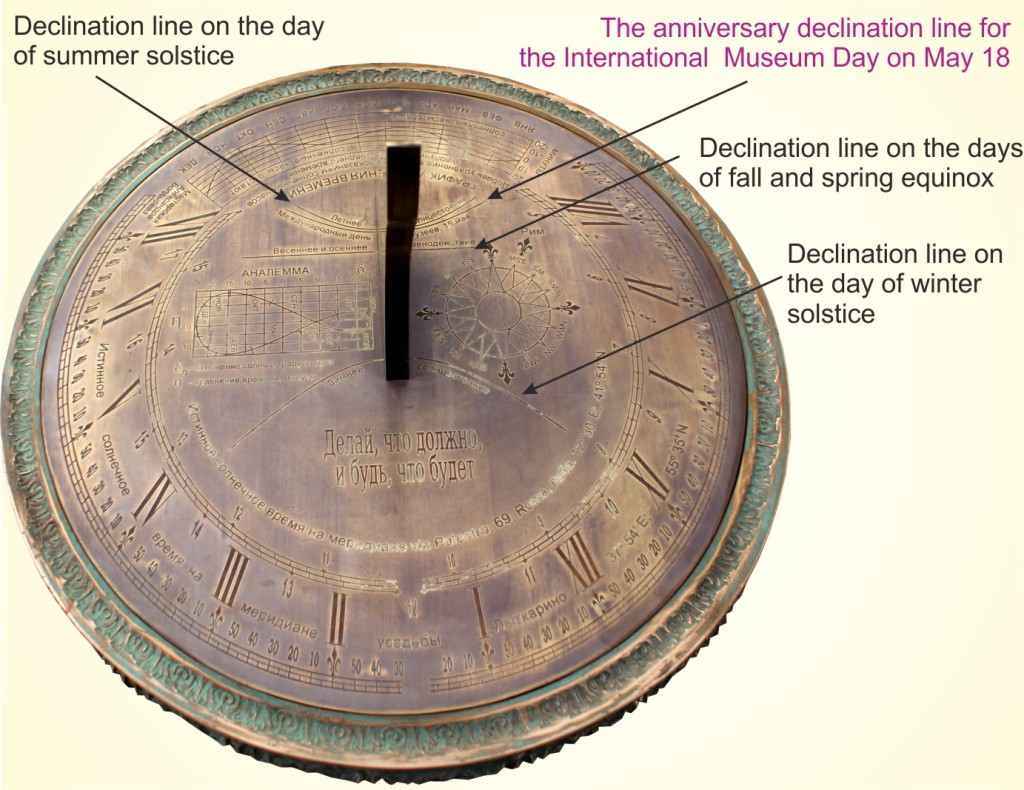
During the year, in every person's life there are many events. Some of them subjectively are more important than changing the Zodiacal months. The declination line calculated for a day that has a special meaning in one’s personal life is called the anniversary line.
Usually the anniversary line is calculated for the wedding day or birthday. But there are many other events worthy of comparison with the position of the Earth in its orbit. For example, the day of the completion of the house, the day the thesis defense, the day of publication of the first poem — it is all very worthy reasons to celebrate them every year with the help of a sundial. On one sundial, you can place more than one anniversary line for each family member or delineate on the sundial more than one dial having its own anniversary line.

Every year on the same day, the sun shadow follows the specially designed anniversary line. This will be while the Solar system exists, that is, in the next four and a half billion years.
What the difference is between the sundial and the clock.
The sundial measures the true local solar time. The clock measures the standard mean time.
The moment when the sun reaches the highest point of its daily path and crosses the local meridian is called the true solar noon. The time interval between two successive noons is called the true solar day.
The true solar day is variable. Some of solar days are longer than others. Consequently, part of them, that is, hours, minutes and seconds are not always equal to each other. It is difficult to construct a time measure machine so that it follows the sun, that is, one day it fasts, the other day it slows. Therefore, the watch measures some other time than true solar time named the mean time. The length of the mean day is obtained by calculation. To do this, the sum of the length of all solar days in the year is divided by the number of days in a year. Therefore, mean days, mean hours, minutes and seconds are constant by definition.
Before the invention of the atomic clock, the most stable unit of time considered to be a sidereal day, determined by the time interval between two successive risings of a some distant star. To measure the length of the true solar day, and then by calculation to determine the length on a mean day, it is traditionally used the sidereal time — sidereal hours, minutes and seconds.
The comparison of the length of the days, expressed in terms of mean time is as follows:
Mean day is 24 h 00 m 00 s
True solar day is 24 h 00 m 00 s ± 17 m
Sidereal day is 23 h 56 m 4,09 s
The axis of the Earth is inclined to the plane of its revolution around the sun at about 23 °. In addition, our planet's orbit has an eccentricity of which it follows that the speed of its revolution around the sun is not constant. For these reasons, the time that falls exactly on the middle of the mean day and called mean solar noon coincides with the true solar noon only four times a year. In the remaining days, the mean noon is ahead of the true solar noon or is delayed as compared to it. This is also true to any moment of time, and not only to noon.
The difference between the true and mean solar time is called the equation of time. In order to measure the mean time on the readings of a sundial it is necessary to take into account the equation of time. In addition, it is usually required do add to the sundial readings the longitude correction and one hour of daylight savings time.
An ordinary watch helps to solve practical problems — not to be late for work, to wake up in time. An ordinary watch is a very useful thing. In a world where the flight schedule and the price of petrol are more real than the Kepler's laws, we can not survive a day without an ordinary watch. Nevertheless, the results of evolution can not be canceled. Our bodies continue to live in true solar time. They still remember how our ancestors felt, making no separating between time and space and between nature and themselves and being happy for this very reason only.
Sundials help us to evaluate our role in the world more abstemiously. They help us to remember that the Earth is a very small planet with limited resources, that it revolves around a small yellow star and that this star is just one of great number of stars making up the Universe — our wonderful home.